Bài tập 5 trang 10 SGK Giải tích 12
Bài tập 5 trang 10 SGK Giải tích 12
Chứng minh các bất đẳng thức sau:
a) \(\tan x > x (0 < x <\frac{\pi }{2} )\)
b) \(\tan x > x +\frac{x^3}{3} (0 < x < \frac{\pi }{2})\)
Phương pháp giải:
Với dạng bài tập ở bài 5 chứng minh \(g(x)>h(x)\) với x thuộc một miền cho trước ta thường tiến hành như sau:
Bước 1: \(g(x)>h(x)\Leftrightarrow g(x)-h(x)>0.\)
Bước 2: Đặt \(f(x)=h(x)-g(x)\), khảo sát tính đơn điệu của hàm số \(f(x)\).
Bước 3: Tìm x để \(f(x)=0\) (thường là hai đầu mút của miền đang xét).
Bước 4: Từ tính đơn điệu của hàm số \(f(x)\) đưa ra kết luận cho bài toán.
Lời giải:
Ta áp dụng các bước trên để giải câu a, b bài 5:
Câu a:
Để chứng minh \(tanx >x\) với mọi \(0 < x < \frac{\pi }{2}\) ta chứng minh tanx - x > 0 với mọi \(0 < x < \frac{\pi }{2}\)
Trước tiên ta cần kiểm tra xem có tồn tại giá trị nào của x đề tanx-x=0 hay không, mà trước hết ta cần thử với hai giá trị là x=0 và \(x=\frac{\pi}{2}.\)
Dễ thấy: \(tan(0)-0=0.\)
Khi đó ta tiến hành mở rộng khoảng đang xét thành nửa khoảng, cụ thể lời giải chi tiết như sau:
Xét hàm số f(x)= tanx–x liên tục trên nửa khoảng \(\left [0;\frac{\pi}{2} \right )\)
\(f'(x) = \frac{1}{{{{\cos }^2}x}} - 1 > 0\) với mọi \(x\in\left ( 0;\frac{\pi}{2} \right )\).
\(f'(x)=0\Leftrightarrow x=0.\)
Bảng biến thiên:
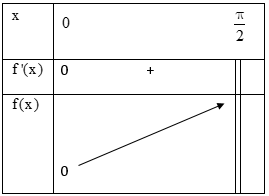
Vậy hàm số đồng biến trên \(\left [0;\frac{\pi}{2} \right )\).
Vậy với \(0 < x < \frac{\pi }{2}\) ta có \(f\left( x \right) > f\left( 0 \right) = 0 \Rightarrow tanx > x\)
Câu b:
Chứng minh \(\tan x > x +\frac{x^3}{3} (0 < x < \frac{\pi }{2})\)
Tương tự câu a.
Xét hàm số \(g(x) = \tan x - x - \frac{{{x^3}}}{3}\) liên tục trên \(\left[ {0;\frac{\pi }{2}} \right)\) có đạo hàm:
\(g'(x) = \frac{1}{{{{\cos }^2}x}} - 1 - {x^2} = {\tan ^2}x - {x^2}\)
\(= (tanx - x)(tanx + x) > 0,\,\forall x \in \left( {0;\frac{\pi }{2}} \right)\) (Theo câu a)
\(g'(x)=0\Leftrightarrow x=0.\)
Bảng biến thiên:
.png)
Vậy hàm số đồng biến trên \(\left[ {0;\frac{\pi }{2}} \right)\).
Vậy với \(0 < x < \frac{\pi }{2}\) ta có \(g\left( x \right) > g\left( 0 \right) \Rightarrow tanx > x + \frac{{{x^3}}}{3}\) với mọi \(x\in\left ( 0;\frac{\pi}{2} \right )\).
Nhận xét:
Với dạng bài tập chứng minh f(x)>0 với x thuộc khoảng (a;b). Nếu f(a) và f(b) đề khác không, hoặc f(x) không xác định tại a và b. Thì f(x)=0 tại x0, với x0 là nghiệm của phương trình f'(x)=0, ta không cần mở rộng khoảng đang xét.
-- Mod Toán 12
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 12
Lớp 12 - Năm cuối ở cấp tiểu học, năm học quan trọng nhất trong đời học sinh trải qua bao năm học tập, bao nhiêu kì vọng của người thân xung quanh ta. Những nỗi lo về thi đại học và định hướng tương lai thật là nặng. Hãy tin vào bản thân là mình sẽ làm được rồi tương lai mới chờ đợi các em!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
